As you extend your hours of procrastination right before math exam day, looking for something cooler to occupy yourself with, why not delve into the world of counterintuitive math paradoxes? Ever heard of Gabriel’s Horn (yes, the Bible was ahead of its time) or Koch’s Snowflake (no, we are not referring to your neighbour who may be in the habit of collecting snowflakes)?
Mathematical paradoxes take us on a ride that traverses the worlds of arithmetic, trigonometry and probability. It is a magical world of fun facts and explanations that are sure to leave you scratching your head, even more than your test day question paper. Who knows, you might just be able to show off some of your math trivia to all those nerds in class who claim to do math for fun. We love encouraging self-learning!
“Few appreciate the role of human curiosity in the evolution of Mathematics as a subject of scientific inquiry.”
It is the innate human desire to seek explanation, predict the future and explore the unknown that has given birth to the mathematical paradoxes and fallacies that we are ranting about. As you keep reading this article, you will be exposed to a whole new world of mathematics in a cultural context that has always existed but seldom observed and acknowledged.
Find your online maths tutor here.
Did you know that the unassuming Pi is also present in our everyday culture?

The Oxymoron that is the ‘Logical Paradox’
You’ll be surprised to learn that Philosophy, as a subject, is far more challenging to grasp than Mathematics is. ‘Paradox’ is “a [logical] statement or proposition which, despite sound reasoning from acceptable premises, leads to a conclusion that seems logically unacceptable or self-contradictory.”
The study of paradoxes deserves a separate class of its own. Though many naturally-occurring paradoxes remain unexplained, there are those others that have been decoded to give us a better understanding of the world around us. We are a little biased towards mathematical paradoxes given their intriguing explanations.
Examples of Mathematical Paradoxes
Zeno’s Paradox
The most historically famous paradox is Zeno’s Paradox. It retells the well-known fable of the hare and the tortoise, in a mathematical language. It was proposed by the Greek philosopher, Zeno of Elea (490 BC 430 BC) who suggested that if the turtle got a head start over the famous Trojan War hero, Achilles, the tortoise would be always ahead in the race. In order to overtake the tortoise, Achilles must first catch up with it. It got tricky, however, every time Achilles caught up with it as there would another gap created between the two.
Perceptions of space, time, motion and infinity hold the key to explaining this paradox. The Standard Solution to Zeno’s Paradox was formulated with the help of calculus, a branch of mathematics that has become an indispensable tool in scientific inquiries of the modern world. You, dear reader, can use it to brush up your logical thinking skills!
Get information on online math tutorial here.

“The Missing Dollar riddle (we’d like to call it a conundrum) is also based on the principles of Zeno’s Paradox.”
The Missing Square Paradox
This one is a mathematical excursion that is sure to give rise to filler games between your school periods!
The Paradox is a logical mathematical hypothesis, based on a visual illusion. And like all illusions, this one too leads us to make an incorrect conclusion. In fact, teachers often use this optical illusion to help students hone their logical reasoning skills. The illusion uses to sets of rearranged geometric sets to construct a triangle. But there is an additional geometric square in the second set. How is that possible?
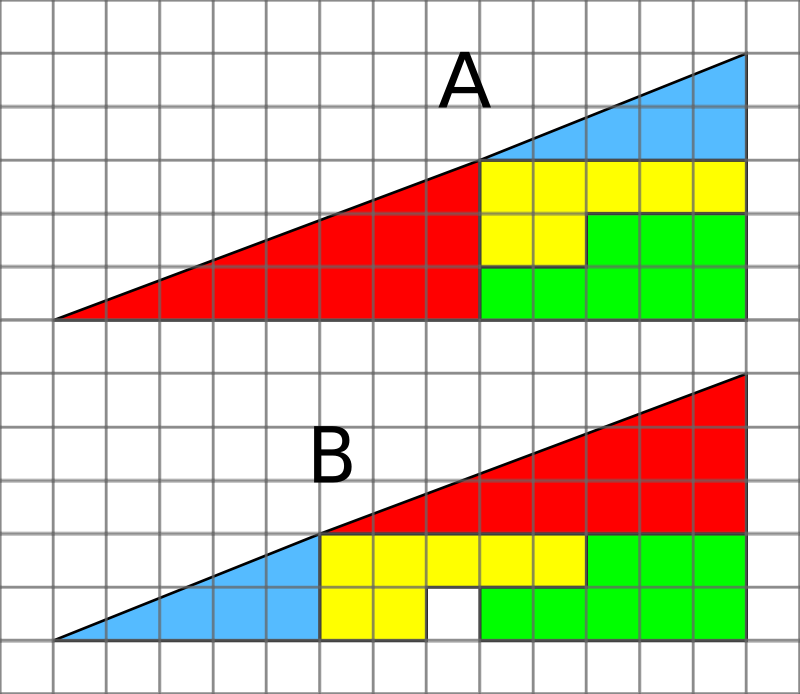
There is actually a simple explanation for this paradox. For starters, allow us to burst your bubble. Neither triangle is a "true" triangle. On closer scrutiny, there appears a slight curve along the hypotenuse of the constructed shape that our eyes perceive to be a triangle. The small empty space is in fact only the result of a small deformation of the perfect triangle with its slightly rounded edges. But, hey! You already knew that, didn’t you?
“Show off your knowledge of mathematical trivia and paradoxes in class. Earn some brownie points from your math teacher. You may need them for your next unit test!”
Impractical Counterintuitive Phenomena
Banach-Tarski Paradox
The Paradox is a geometric theorem that states how a 3-dimensional ball may be finitely decomposed into many pieces and then reassembled to produce two copies of the original ball. Hmm…and we thought J.K. Rowling lived in an imaginary world, far removed from reality!
The assertion that the original volume of the ball can be doubled simply by cutting it up into finite pieces makes it a counterintuitive phenomenon. It is a fact that the decomposed pieces lack well-defined volumes. Their existence depends on the axiom of choice.
Mad Scientists Rule the Roost
In 1929, John von Neumann, an epitome of the mad scientist ideal (no, he was not clinically mad, perhaps, a mad genius) decided to go one step further than the Banach-Tarski Paradox. He decomposed a square into a (finite) number of 'sets of points' and then reassembled them to obtain two squares! Decades later, another eccentric genius, Miklós Laczkovich provided an explanation for von Neumann’s paradox in 2000.

Barber's Paradox
If you are not infuriated or frustrated enough already, here is another logical paradox that might just do the trick! Proposed by Bertrand Russell in the early 1900s, the paradox talks of a town in which all the residents need to be clean-shaven (not a place where you’d like to venture into?). Now, you may question the soundness of this query – who cares if a town has clean-shaven residents, or not? Moving on, the town barber takes it upon himself to shave everyone. The more important question now becomes: who shaves the barber?
“The answer to the barber paradox is just that, the statements themselves are false.”
Russell, by his own admission, later on, created the paradox and threw open some questions to test people’s understanding of logical theories such as groups and classes of people. To quote him, the Barber Paradox “is just noise without meaning.” We don’t blame you for believing old Mr Russell was deriving sadistic pleasure out of this. But, really, this is a really useful exercise to polish your sense of logic.
Turning the Earth Inside Out!
Next, we move on to the world of differential and linear topology. In 1958, S. Smale formulated what is called ‘sphere inversion (or reversal)’. The law asserts that it is possible to turn a sphere inside-out through continuous deformation without causing the sphere to puncture, rip open, and develop creases or pinched surface.
“With the advent of computer animation, Smale’s sphere inversion has become a reality, at least in a 3-dimensional virtual space.”
Know of any other mathematical mysteries?
Everyday Counter-Intuitive Phenomena
Simpson Paradox
The paradox, also known as the Yule-Simpson Effect was formulated by statistician Edward Simpson in 1951. In this paradox, a trend that appears across several different data sets tends to disappear or get reversed when these data sets are combined.
Imagine a scenario in which a college administration, concerned about gender bias in their admission process, classifies applicants based on their sex. The resultant data would likely indicate a gender bias where more males are admitted than females.
The college further divides applicants based on the department they applied to (natural or social sciences, for example). The resultant data reveals a reversal of outcomes where females were more likely to be admitted to the natural sciences department than men.
“Simpson Paradox is more straightforward than it appears at first glance. Therefore, it has found many real-world applications to demonstrate how pooled data results might differ from individualized tests.”
Condorcet’s Rule
The Condorcet Rule is a voting methodology designed to elect a candidate with a majority of the votes in all head-to-head elections against each of the other candidates. The candidate who wins this way is called the Condorcet winner.
The Condorcet election methodology has been named after the 18th-century French mathematician and philosopher, Marie Jean Antoine Nicolas Caritat, the Marquis de Condorcet, a staunch advocate of this style of voting.
The Condorcet system of voting essentially allows voters to rank their preferences for candidates. This way, voters don’t have to worry about having to vote for a candidate with little or no chance of winning. One would wonder why this rule has not gained more popularity in democracies across the globe.
Need help learning about maths concepts? Find a professional maths teacher on Superprof!
“Do you think the Condorcet Rule can work in India?”

Now that you have some idea about mathematical paradoxes and fallacies, how do they compare with some of the frustrating problems you might be facing in real life? Hope, that is inspiration enough for you to get over your procrastination and get down to the business of the mathematics exam due soon!
On a much lighter note, here is how two mathematics teachers, led on by their curiosity, discovered the main protagonist in Game of Thrones, using, yup, you guessed it right...mathematics.















You forgot to specify “THEMSELVES” in the barber paradox. As it stands, there’s nothing paradoxical in your version of the barber paradox.